力扣120题**攻略：动态规划解三角形最小路径和（C++实现）

ftggdnt

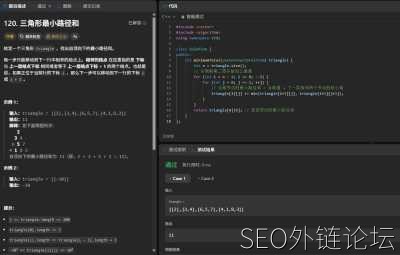
问题描述

给定一个三角形 triangle ，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的节点上。

C++解决方案（带注释）

1. #include <vector>
   
2. #include <algorithm>
   
3. using namespace std;
   
4. 
   
5. class Solution {
   
6. public:
   
7.     int minimumTotal(vector<vector<int>>& triangle) {
   
8.         int n = triangle.size();
   
9.         // 从倒数第二层开始向上递推
   
10.         for (int i = n - 2; i >= 0; --i) {
    
11.             for (int j = 0; j <= i; ++j) {
    
12.                 // 当前节点的最小路径和 = 当前值 + 下一层相邻两个节点的较小值
    
13.                 triangle[i][j] += min(triangle[i+1][j], triangle[i+1][j+1]);
    
14.             }
    
15.         }
    
16.         return triangle[0][0]; // 返回顶点的最小路径和
    
17.     }
    
18. };

复制代码

算法解析

• 动态规划思想：采用自底向上的方法，避免重复计算
• 时间复杂度：O(n²)，其中n是三角形的行数
• 空间复杂度：O(1)，直接在原数组上修改
  
  

优化思路

• 可以使用一维数组进一步优化空间复杂度
• 边界条件处理：当三角形为空时直接返回0
  
  

链接：动态规划